A structural metric is defined as an equation describing a relationship between the conductivity of a target element and one of the following:

1. the conductivity of the target element's neighbor
2. the specified reference conductivity value (see v_ref in the inverse options file syntax)
3. the conductivity of the corresponding element specified in the reference model file

When a particular structural metric is specified to a zone, E4D applies that metric to every element in that zone, and optionally to elements bounding that zone if so specified in the corresponding constraint block. E4D attempts to minimize each structural metric, which imposes some desired structure in the inverse solution.

E4D determines the conditions under which to apply the constraints according to the weighting function applied to each structural metric. Thus the behavior of each structural metric in terms of constraining the inversion is also dependent upon the corresponding weighting function for that metric. In the table below, equations are shown defining each structural metric.

Structural metric code (s_met)	Equation	Intepretation
1	X=mt-mn	The difference between the log conductivity of the target element mt and the log conductivity of the target element's neighbor mn
2	X=|mt-mn|	The absolute difference between the log conductivity of the target element mt and the log conductivity of the target element's neighbor mn
3	X=mt-v_ref	The difference between the log conductivity of the target element mt and the log conductivity of the neighbor's reference value vref, taken from either the constraint block or converted from the reference model file
4	X=|mt-v_ref|	The absolute difference between the log conductivity of the target element mt and the log conductivity of the neighbor's reference value vref, taken from either the constraint block or converted from the reference model file
5	X=mt-mn	Same as 1 but with anisotropic weighting
6	X=|mt-mn|	Same as 2 but with anisotropic weighting
7	X=(mt-v_reft) - (mn-v_refn) or X=Dmt - Dmn	Typically used for time-lapse inversion: the difference between the temporal change in log conductivity among spatially adjacent elements, where the temporal change for a given element is the log conductivity of that element minus the log conductivity of the same element at some reference time, vref. Dmt is the change in log conductivity of the target element with respect to v_reft. Dmn is the change in log conductivity of the neighbor element with respect to v_refn.
8	X=|(mt-v_reft) - (mn-v_refn)| or X=|Dmt - Dmn|	Typically used for time-lapse inversion: the absolute difference between the temporal change in log conductivity among spatially adjacent elements, where the temporal change for a given element is the log conductivity of that element minus the log conductivity of the same element at some reference time, vref. Dmt is the change in log conductivity of the target element with respect to v_reft. Dmn is the change in log conductivity of the neighbor element with respect to v_refn.
9	X=mt-mn	Same as 1 but applied only at specified boundaries
10	X=|mt-mn|	Same as 2 but applied only at specified boundaries

The primary purpose of the weighting function is to determine the conditions under which the corresponding structural metric should or should not be used to constrain the inversion. In essence, the weighting functions turn the structural metrics on and off, and determine how much weight should be placed on minimizing the structural metric in the transition between on and off.

The independent variable for each weighting function is the value of the structural metric (i.e., the value X in the structural metric code table). Each of the four weighting functions is based on the normal and cumulative normal distribution functions, and ranges between 0 and 1. If the weighting function evaluates to zero, then the structural metric is inactive and plays no role in constraining the inversion. If it evaluates to one, then the structural metric is fully active. The following table and figures show the equation and form of each weighting function.

Weighting Function Code (fw)	Equation	Graph
1		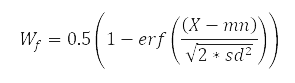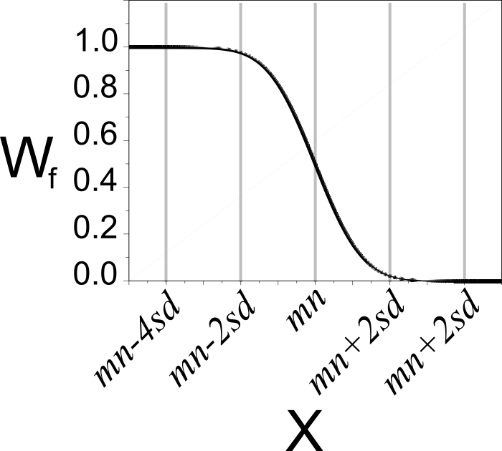Minimize X if X drops below mn+2sd, reaching full weight if X drops below mn-2sd.
2		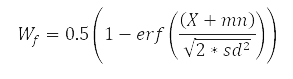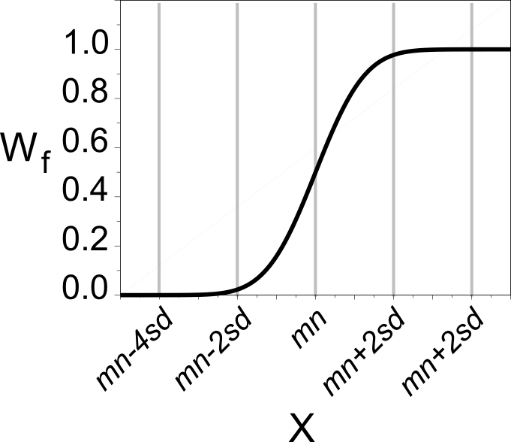Minimize X if the value of X rises above mn-2sd, reaching full weight if X rises above mn+2sd.
3		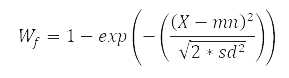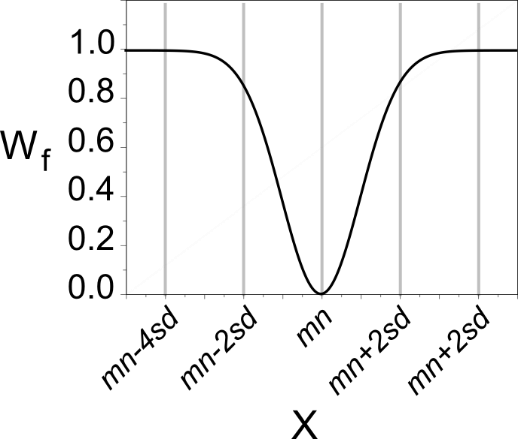Minimize X if the value of X deviates from mn, reaching full weight if X deviates from mn by more than (approximately) 2sd
4		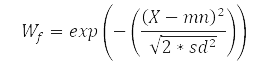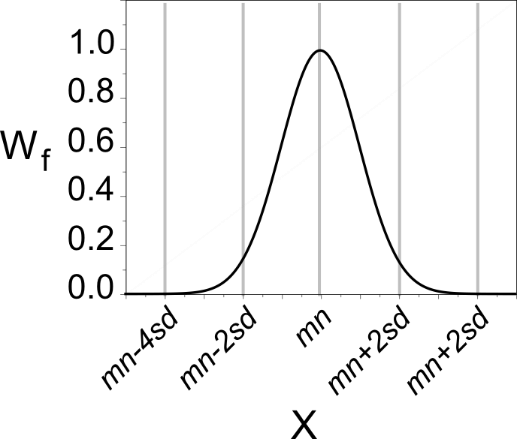Minimize X as the values of X approaches mn, reaching full weight when X is equal to mn.
Variables: Wf = value of the weighting function where (0 <= Wf <= 1) X = value of the structural metric (see structural metric code table) erf = error function exp = exponential where e = 2.718281828 mn = mean of the weighting function as specified in the constraint block in the inversion options file sd = standard deviation of the weighting function as specified in the constraint block in the inversion options file